皆さんこんにちは。

更新がかなり遅くなりまして申し訳ありません。以前の記事で消防設備士試験を受ける人がいるので～というのを紹介しましたが、この試験対策が完結する前に試験を迎えてしまいました。関係者の方々には申し訳なく思います。ですが続いているこの試験対策シリーズを途中で終わりにするのもどうかと思いとりあえず完結させるべく頑張ります。今回は機械に関する基礎的知識をやっていきます。

出題傾向として

この機械に関する基礎的知識からは５問出題され、そのうち最低２問は正解しないと不合格になります。

科目としては「応用力学」「機械材料」「気体・水理」の３つがあり、計算をして解答を選ぶ問題や、言葉の定義から解答を選ぶ問題が出題されます。計算する問題では計算機などは使えない（持ち込めない）ので簡単な計算や暗算で答えを出せる問題になっています。

ただ簡単な計算で～とはいいましたが、公式を覚えておかないと計算できないのでやはり易しくはありません。

応用力学

ここでは「力の三要素」や「力のモーメント」などの力に関する定義になります。工業高校などで機械分野を勉強した方なら聞いたことがある問題になります。

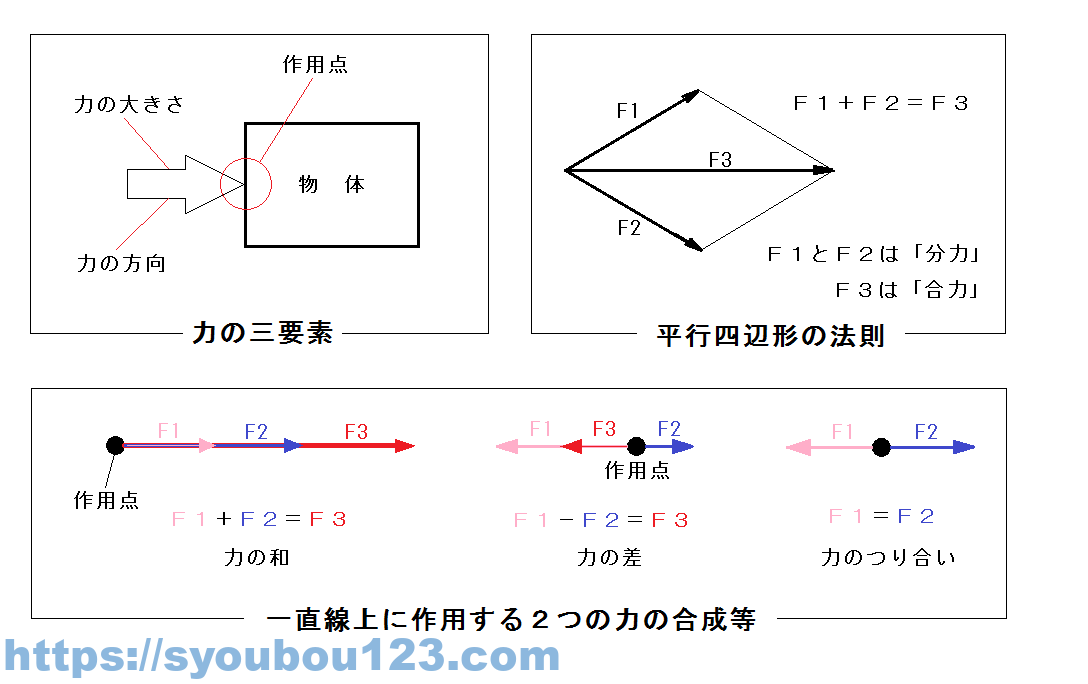
（１）力の三要素

物を動かしたり、止めたり、速さを変えるのに必要なものが力である。この力の強さを決定するのに以下の３つがある。

大きさ（力の大きさ・強さ。）
方向（どの方向に力が作用しているか。）
作用点（物のどこに力が作用しているか。）

上記の３つ（力の大きさ、力の方向、力の作用点）を力の三要素といいます。

（２）力の合成・分解・つり合い

一つの点に作用する力（分力という）が２つ以上あるときは、その２つ以上の力を合わせて（合成）して一つの力に表すことができ、この合成した力を「合力」といいます。

２つの力が一直線上に作用するときの合力は、２つの力が同じ方向であれば和になり、２つの力の方向が反対なら差になる。この反対向きの力の大きさが等しいときは合力は０になり、お互いの力が作用していなのと同じ現象が起こる。これを力のつり合いという。

また、一つの点に２つの力（Ｆ_１とＦ_２とする）が作用すると、このＦ_１とＦ_２の２辺は平行四辺形の対角線（Ｆ_３とする）に等しい力になる。これを「力の平行四辺形の法則」という。

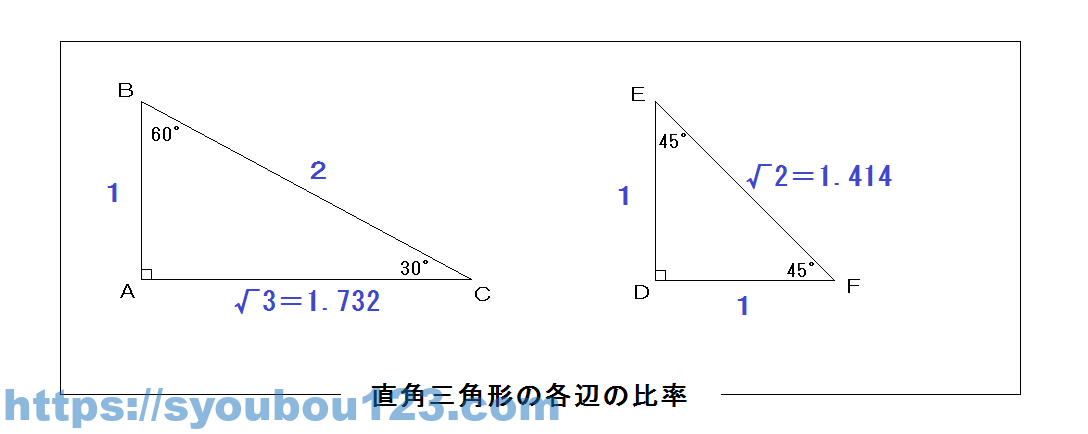
この力の大きさは、「三平方の定理」（ピタゴラスの定理）（直角三角形の斜辺の２乗は他の２辺の２乗の和に等しいという法則）を用いれば計算にて求めることができるので、角度が３０°、４５°、６０°の比率を覚えておくと良い。この法則を逆にすれば１つの力をそれぞれ角度を持つ２つ以上の力に分けることもできる。これを「力の分解」という。

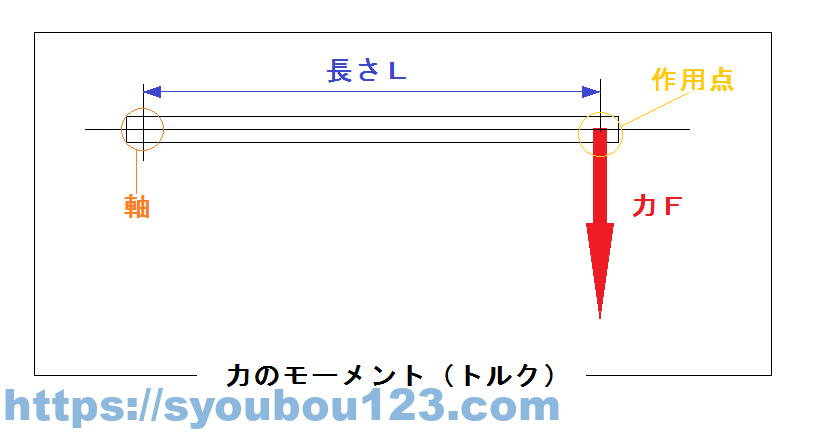
力のモーメント

モーメントとは、力が物体を回転させるときに回転軸を中心に回転しようとする力の働きを言う（トルクともいう）。モーメントＭ（N・ｍ）は、加えられる力Ｆ（N）と、軸から力の作用点までの距離Ｌ（ｍ）との積（Ｍ=ＦＬ）により求めることができる。

このモーメント（トルク）は、ボルト（ナット）の締付け力などの計算などにも用いられているので覚えておいて損はないと思います。出題回数も多い傾向にあるみたいです。

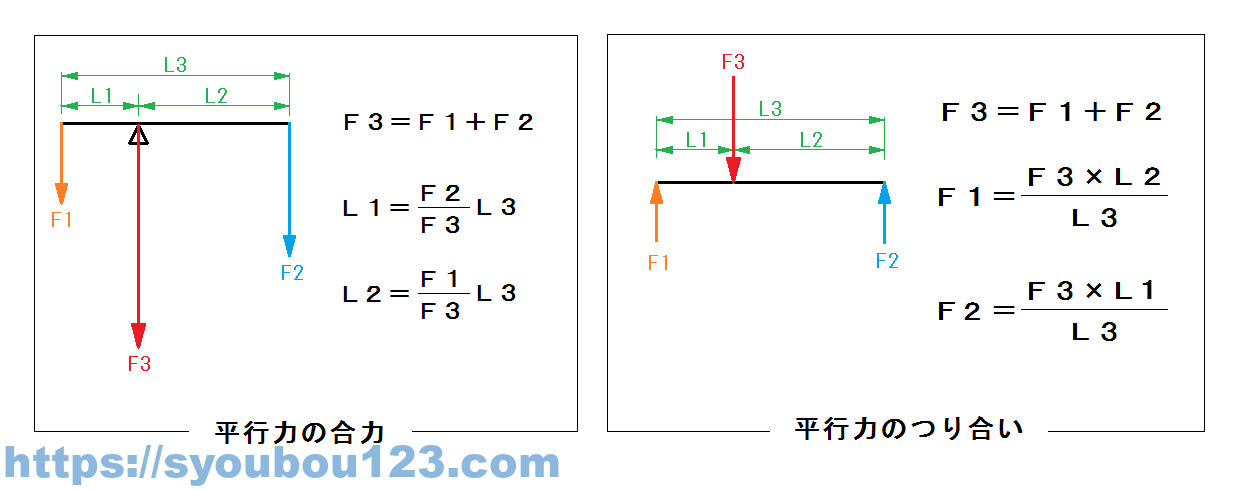
平行力の合成・つり合い

１つの直線上に２つ以上の平行な力が作用している時も、力の合成をすることができる。また合成とは逆に、力が作用している時にその力に逆らって作用する力があったとき、それぞれの荷重の差が等しい時に合力が０になる。これを平行力のつり合いという。

摩擦力

動いていない（静止している）物体に力を加えたときに、その物体が動き出すときの力を最大摩擦力（単純に摩擦力という場合もある）という。この最大摩擦力（Ｆ）は、物質の接触面に垂直にかかる圧力（Ｗ）に摩擦係数（μ）の積（Ｆ=μＷ）で求めることができる。式を分解すると、μ=Ｆ／Ｗになる。

ちなみに摩擦係数のμは、接触面の状態や材質により決まる係数になり、接触面の大小は関係ないので注意してください。

速度・加速度

（１）速度

物体が一定時間にどれだけ変位（位置の変化）したかという変化の度合い。小学生の時に習った速さの問題と同じ。速さ=距離／時間

速度ｖ=変位ｓ／時間ｔ　変位ｓ=速度ｖ✕時間ｔ

（２）加速度

一定時間に起こる速度が変化する割合のことをいう。例えば現在１０ｍ／秒で走っている車が１秒後に２０ｍ／秒に加速したら、加速度は１０ｍ／秒^２になります。もちろん速度に変化がなければ加速度は０になります。式にすると

加速度ａ=（変化後速度ｖー変化前速度ｖ_０）／時間ｔ（ｍ／ｓ^２）

（３）落下速度

物質をある一定の高さから落とした（落下させた）時に、物質は加速度を生じながら落下する。この速度を落下速度といい、自由落下、投げ上げ、投げ下ろしの３つがある。

速度ｖ、重力加速度ｇ（9.8m/s^２）、時間ｔ（秒）、初速ｖ_０、変位ｙとしたときに、

自由落下は、速度ｖ = ｇ✕ｔ、変位ｙ = （ｇ✕ｔ^２）／２

投げ上げは、速度ｖ = ｖ_０ーｇ✕ｔ^２、変位ｙ = ｖ_０ｔー（ｇ✕ｔ^２）／２

投げ下ろしは、速度ｖ = ｖ_０+ｇｔ、変位ｙ = ｖ_０ｔ+１／２ｇｔ^２

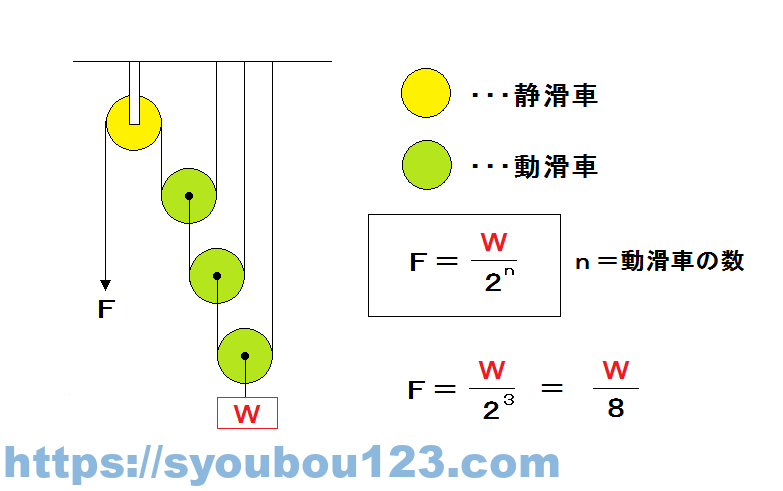
滑車

天井から吊り下げられている、ロープなどの動きに追従しない（動かない）滑車は「定滑車」という。それ以外でロープなどの動きに追従する（動く）滑車を「動滑車」という。この動滑車一個につき必要な力は半分になるが、仕事量は変わらない。

荷物の重さをＷ（Ｎ）、ロープを引く強さをＦ（Ｎ）、動滑車の数をｎ（個）とした場合に

Ｆ＝Ｗ／２^Ｎ

になる。動滑車が３個ならＦ＝Ｗ／８となる。

滑車の例

仕事と動力

（１）仕事（仕事量）

１つの物体に力（Ｆ）が作用してｓだけ移動したときに、力（Ｆ）はその物体に仕事をしたという。

仕事量Ｗ=Ｆ✕ｓ（Ｊ）又は（Ｎ・ｍ）

Ｎ（ニュートン）は力の大きさを表す単位。
１Ｎは、１（Kg） ✕ １（ｍ／ｓ^２）

Ｊ（ジュール）は仕事（仕事量）の単位。
１Ｊは、１（Ｎ）✕ １（ｍ）

（２）動力

一定時間（単位時間）にする仕事の量を動力（仕事率や効率ともいう）という。

単位時間ｔ、仕事量Ｗ、動力Ｐとすると

動力Ｐ = Ｗ／ｔ（Ｎ・ｍ／ｓ）

Ｗ（ワット）は動力の大きさの単位。
１Ｗ = １Ｊ／ｍ

また動力は加えられた力と速度の積でも求められる。

動力Ｐ = Ｆ✕ｖ　（速度ｖはｍ／ｓ）

荷重

物体に外部から作用する力を「荷重（かじゅう）」という。荷重を受けると物体は変形し、荷重が大きくなり過ぎると物体は破壊されてしまう。荷重には以下の種類がある。

（１）荷重の加わり方による種類

静荷重･･･一定の大きさ（力の向きと大きさが変わらない）の状態を続ける荷重。
動荷重･･･力の向きや大きさが変動する荷重で、以下の３種類ある。
1. 繰り返し荷重･･･向きは同じだけど力の大きさが変わる。
2. 交番荷重･･･向きと力の大きさが時間によって変わる。
3. 衝撃荷重･･･運動状態が急激に変化し、短時間に加わる荷重。

（２）荷重の作用による種類

引張り荷重･･･引き伸ばす様に作用する荷重。
圧縮荷重･･･押し縮める様に作用する荷重。
せん断荷重･･･ハサミで切るように作用する荷重。
曲げ荷重･･･曲げるように作用する荷重。
ねじり荷重･･･ねじる様に作用する荷重。

荷重の種類の例

応力

物体に外部から力が加わると、それに応じて物体の内部に反対向きで抵抗する力が生じる。これを「応力」という。この応力には以下の種類がある。

引張り応力
圧縮応力
曲げ応力
せん断応力
ねじり応力

また、単位面積に対する応力の大きさを「応力度」といい、単純応力（引張り、圧縮、せん断など）は荷重を物質（材料）の断面積で徐して求める。

応力（Pa）＝荷重／断面積

ちなみに応力の単位はPa（パスカル）で

１Pa＝１Ｎ／ｍ^２
１ＭPa＝１Ｎ／ｍｍ^２
１ＭPa＝10⁶Pa

ひずみ

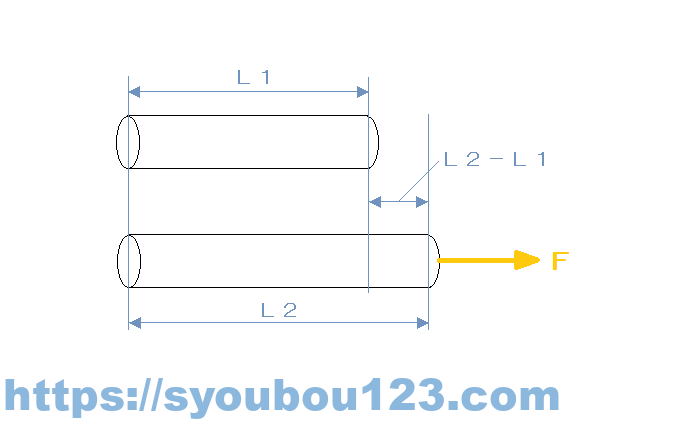
物質に荷重が加わると物質は形が変わる（変形する）。この時の変形量と変形前の比率をひずみという。

ひずみをｅとすると、ｅ＝(L2-L1)／L1 になります。

ひずみの例

応力とひずみ

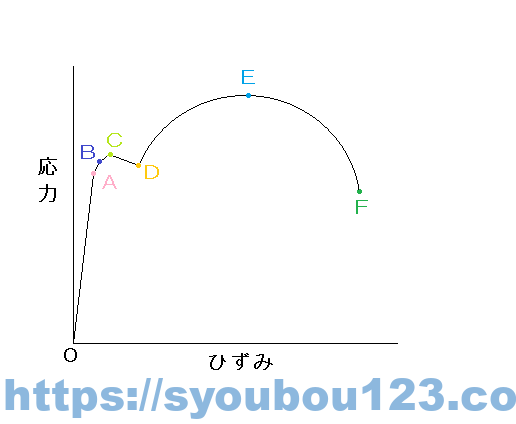
試験片（テストピース）に引っ張り荷重を加え、試験片が破壊（破断）するまで引っ張った荷重と試験片の伸び量の関係をグラフに表したのが応力ーひずみ曲線図というグラフになります。このグラフを見てみると

応力－ひずみ曲線図

Ａ…応力とひずみが比例する限度（比例限度）

Ｂ…荷重を取り除けば伸びも戻る限度（弾性限度）

Ｃ〜Ｄ…応力が増加しなくてもひずみが急増する部分（Ｃ：上降伏点、Ｄ：下降伏点）

Ｅ…最大荷重の時の応力（極限強さ）

Ｆ…破壊点

ちなみに０からＡ点までの間は荷重と伸びが正比例するので、フックの法則が成り立つ。フックの法則とは、荷重と伸びが正比例することである。

許容応力と安全率

許容応力とは、使用する材料が変形や破壊などをせず安全に使用することができる最大応力のことで、許容応力は極限強さを安全率で割って求めることができる。

許容応力 = 極限強さ／安全率

安全率 = 極限強さ／許容応力

梁（はり）の種類

梁には以下の種類があります。

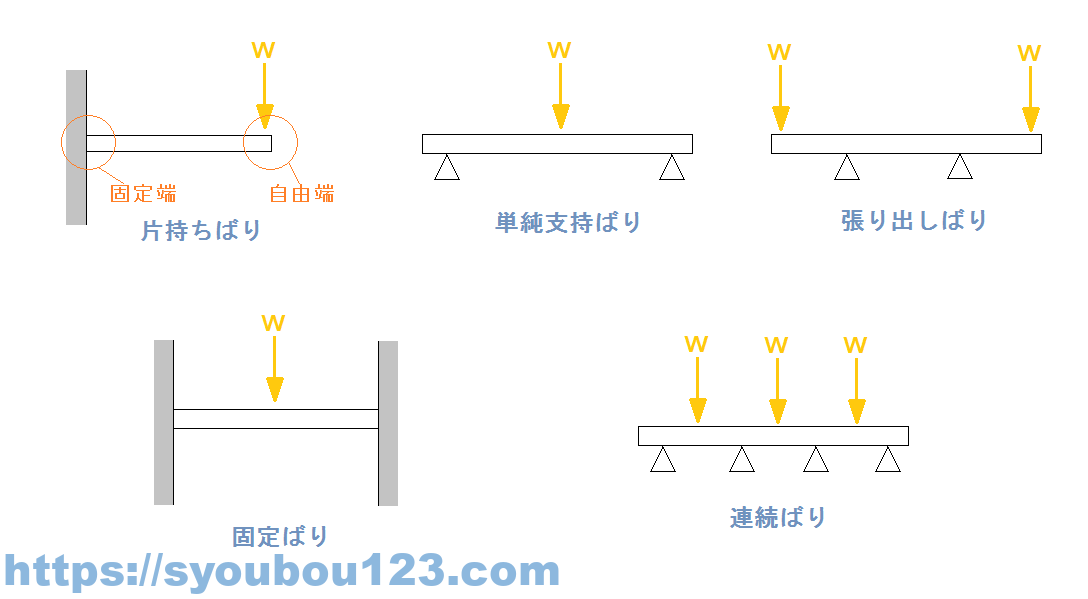
（１）片持ちばり

片方の端を固定して、もう片方の端は固定しないで自由に突き出ているはりのこと。固定されている端を固定端といい、固定されていない端を自由端という。

（２）単純支持ばり

両端をそれぞれ一個の支点でささえているはりのこと。両支えばりともいう。

（３）張出しばり

支点の外側に荷重がかかっているはりのこと。

（４）固定ばり

両方の端が固定されているはりのこと。

（５）連続ばり

支点が３個以上あるはりのこと。

はりの種類の例

機械材料

ここでは、金属の性質や合金、熱処理といった金属材料に関する部分になります。これも工業科などで勉強したことがある方がいると思います。

金属の性質

金属には以下の性質があります。

水銀を除き、常温で固体である。
叩くと平面的に広がる性質（展性）や伸ばすと伸びる性質（延性）があり加工が容易である。
金属的光沢がある。
電気や熱を通しやすい（良導体）（伝導性が良い）。
加熱すると膨張する（膨らむ）。膨張率が一番高いのは鉛。
融点（溶ける温度）が高い。融点が一番低いのはすず、一番高いのはタングステン。
比重はそれなりに高い。一番低い（軽い）のはマグネシウム、一番高い（重い）のは白金。
高温で溶けて、常温では固まる性質を利用して溶けた金属を金型などに入れて成形することができる（可鋳性がある）。
加熱してから叩くと成形が容易にである性質がある（可鍛性がある）。
腐食のしやすさ（耐食性）は、一般的に金属は腐食するが白金と金は腐食しない性質がある。またアルミニウムやすずなどは表面に酸化皮膜があり腐食が内部にまで浸透しない金属もある。

ちなみに伝導性が良い金属は

銀＞銅＞アルミニウム＞タングステン＞鉄

合金

金属に他の金属を混ぜ合わせてお互いの特性を生かした金属を合金といい、ステンレス鋼や黄銅、炭素鋼などがそうです。金属を合金にした時の性質には以下がある。成分金属とは合金に含まれている金属の成分（ニッケルやクロム、マンガンなど）のことである。

比重と膨張率は、成分金属の割合から求めた数値にほぼ同じである。
融点は、成分金属の平均値よりもだいたい低い。どの合金よりも融点が低いものの代表としてハンダ（半田）があり、半田はスズと鉛の合金である。
引張り強さ（抗張力）は、一般的な成分金属より強くなる傾向にある。
硬さ（硬度）は、成分金属よりも増加する傾向にある。
熱や電気の伝導率は、成分金属の平均値よりも低くなる傾向にある。
可鋳性は、成分金属よりも増加する傾向にある。
可鍛性は、減少若しくは全く０になるものもある。
耐食性は、著しく増加する傾向にある。

主な合金とその成分

（１）鉄との合金

純鉄…炭素含有量がほぼ０の鉄をいう。
炭素鋼…炭素含有量が0.02〜2%のもので、炭素含有量が多いと引張り強さと硬さは増えるが、伸び率・衝撃率は減る。炭素含有量の多いものは工具鋼やばね鋼として用いられる。
鋳鉄…炭素含有量が2〜6.7%のもので、耐摩耗性・可鋳性・圧縮強さに優れるが非常食にもろい（衝撃に弱い）。
合金鋼…鉄に合金元素を含有させて、鋼の性質を向上させたり、所定の性質をもたせている合金のことで強度や耐熱性や耐食性に優れている。代表的な合金鋼としてステンレス鋼があり、ステンレス鋼は鉄に炭素・クロム・ニッケルなどを混ぜ合わせたもので、クロムステンレスやニッケル・クロムステンレス（18-8ステンレス）などの種類がある。

（２）銅との合金

銅との合金には黄銅、青銅、白銅などがあり、熱・電気の伝導性が良く圧延性や伸延性に優れている。黄銅は銅と亜鉛の合金で真鍮とも呼ばれている。青銅は銅とすずの合金で砲金とも呼ばれている。白銅は銅とニッケルの合金で硬貨に使われている。

（３）アルミニウムとの合金

アルミニウム単体では比重が軽くて、熱・電気の伝導率が高く、展延性や耐候性に優れているが、酸やアルカリ溶液や海水などには弱く、耐熱性や強度が劣る。その為ジュラルミンに代表されるようにアルミニウムに銅やマグネシウムやシリコンを含有させて強度や耐食性を上げたりしてアルミニウムの軽さを活かしつつ強度があるのがアルミニウム合金になります。

熱処理

鉄や鋼、その他の金属に必要とする性質を付与する為に行う加熱・冷却を行う処置のことで、強度や展延性を向上させたりできる。熱処理の種類は多種にわたるが、代表的な処理を以下で説明します。

（１）焼入れ

鋼などを所定の高温に加熱した後に、油中や水中で急冷させることにより金属組織を変化させて強度や引張り強さを向上させることができるが、靭性が低下する（粘りがなくなり脆くなる）。

（２）焼戻し

焼入れを行うなどして不安定な金属組織になった金属を適切な温度に加熱して、徐々に冷ますことで不安定になっていた金属組織を安定させて靭性を回復させる（粘りを戻して脆さをなくす）処理のことである。焼入れ→焼戻しの工程が一般的である。

（３）焼きなまし

加工硬化により生じた内部ひずみを取り除いたり安定した金属組織にする為に、加熱処理を一定時間行った後に炉内などでゆっくり冷まして行く処理のことである。

（４）焼きならし

金属組織を均一にしたり内部残留応力を除去したりするために、所定温度まで加熱した後に空中放冷によりやや早めに冷却を行う。焼きなましよりも冷却速度は速い。

ねじ（ボルト・ナット）

（１）ねじの種類

国際標準化機構（ＩＳＯ）が国際規格として採用した直径やピッチをミリメートルで表したねじがメートルねじで、インチで表したねじがインチねじであり、日本では原則としてメートルねじが使われている。山の角度が６０°の三角ねじで並目と細目がある。細目とは並目よりもピッチが細かいねじのことである。

（２）メートルねじの呼び方

ねじにはおねじとめねじがあり、おねじの山の外形（ｍｍ）の大きさ（数値）にＭをつけて表示する。外形が１０ｍｍならＭ１０になる。めねじは、谷の内径の大きさにＭをつけて表示する。

ピッチは山と山（谷と谷）の距離のことで、山と山の距離が１ｍｍならピッチは１になる。

例えばＭ10‐1.25なら、ねじの外形が１０ｍｍで、ピッチが1.25ｍｍのねじを表す。

おねじとめねじの例

気体と水理

ここでは気体や水（油）に関する法則や原理を説明していきます。ボイル・シャルルの法則やパスカルの原理などが出てきます。

気体

（１）大気圧とゲージ圧力

大気圧とは、地球上に常に空気の重さにより加わっている圧力のことをいう。標準大気圧は、101325Pa（パスカル）でおよそ0.1MPaになる。

また、この大気圧を基準に用いられる圧力にゲージ圧力がある。大気圧を０として真空方向に働く大気圧より低い圧力（負圧）を示すのが真空ゲージ圧力といい、その反対の方向で大気圧より高い（正圧）圧力をゲージ圧力という。例えば自転車のタイヤの空気圧はゲージ圧力になり、大気圧よりも大きい圧力がタイヤの中に入っているからです。

その他に絶対圧力というものがあり、完全真空を基準に圧力を表示する圧力のことをいう。絶対圧力はゲージ圧力に大気圧（0.1MPa）を足した値である。

（２）絶対温度

私達が普段使っている温度は摂氏といいます。体温はおよそ摂氏36℃、水が沸騰するのは１気圧で摂氏100℃になりますが、この摂氏で-273.15℃という原子も分子も活動を停止する温度を絶対零度といいます。この絶対零度を基準（０）にして表す温度に絶対温度（ケルビン）［Ｋ］があり、絶対温度（Ｋ）＝２７３ + 摂氏温度（℃）になります。

（３）ボイル・シャルルの法則

（Ａ）ボイルの法則

温度を一定にしたときに、気体の体積は圧力に反比例するという法則。

・Ｐを気体の圧力

・Ｖを気体の体積

・ａを定数

とすると、

ＰＶ＝ａ　若しくは　Ｐ1Ｖ1＝Ｐ2Ｖ2＝ａ　となる。

（Ｂ）シャルルの法則

圧力を一定にしたときに気体の体積は絶対温度に比例するという法則。

・Ｖを気体の体積

・Ｔを絶対温度

・ａを定数

とすると

ａ＝Ｖ／Ｔ　若しくは　Ｖ１／Ｔ１＝Ｖ２／Ｔ２＝ａ　となる。

（Ｃ）ボイル・シャルルの法則

気体の体積Ｖは圧力Ｐに反比例して、絶対温度Ｔに比例するというボイルの法則とシャルルの法則が合わさった法則である。定数をａとすると

ＰＶ／Ｔ＝ａ　若しくは　Ｖ＝Ｔ／Ｐ

また気体の状態が変化した時に

変化前の圧力をＰ1、体積をＶ1、温度をＴ1

変化後の圧力をＰ2、体積をＶ2、温度をＴ2

とした場合に

Ｐ1Ｖ1／Ｔ1＝Ｐ2Ｖ2／Ｔ2　となる。

水理

（１）パスカルの原理

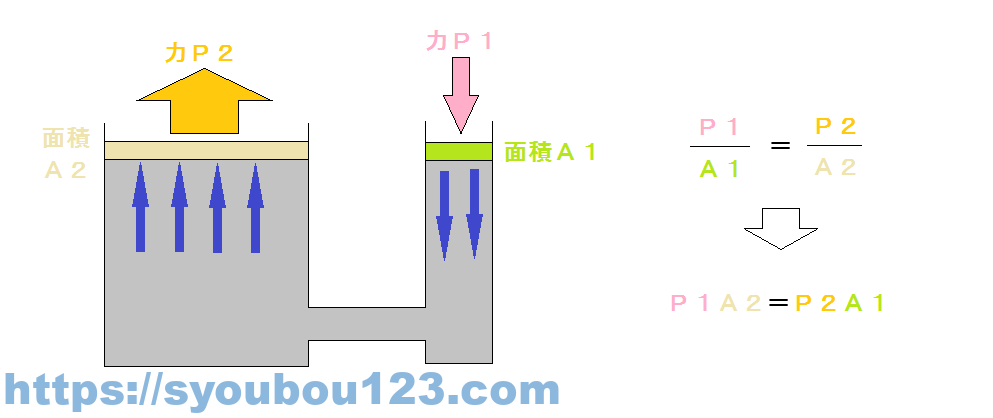
密閉された容器内の流体は、その容器の形に関係なく一点に受けた単位面積当たりの圧力をそのままの強さで流体の各部分に伝えるという流体静力学の基本原理をパスカルの原理という。

下図を参照していただき、Ａ1、Ａ2をピストンの断面積、Ｐ1をＡ1のピストンに加える力、Ｐ2をＡ2のピストンに伝わる力とすると図中の式が成り立つ。

パスカルの原理

小さい力を小さい面積に加えて、大きい面積に大きい力を発生させることができるので、この原理を身近に利用したものに油圧ジャッキなどがある。

（２）アルキメデスの原理

静止した流体中にある物体は、その物体が排除した（押しのけた）流体の重量に等しい大きさの浮力（鉛直上の向きの力）を受けるという原理をアルキメデスの原理といいます。

別の表現で言うと、物体に働く浮力は物体が占めている部分を流体に置き換えたときにその流体の塊に働く重力と同じになる。という原理。

まとめ

最後までご覧いただきありがとうございます。

前回の更新からおよそ１ヶ月がすぎてしまい、皆様には御迷惑をおかけしまして申し訳ありませんでした。今回の内容は消防設備に限らず、いろいろな分野で活用できると思うので覚えておいて損はないと思います。特にモーメント、滑車、ねじ（ボルト・ナット）は覚えておきましょう。

今回は乙種６類という分類で説明していますが、この機械に関する基礎知識は消防設備士１類・２類・３類・５類でも共通なので６類に限らず御活用いただけます。